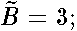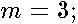Recent technological progress in fabrication of semiconducting and metallic nanostructures opened a vast field of research of their electron properties [1, 2]. Traditionally application of high magnetic fields is an extremely powerful method for experimental studies of electronic properties in solids. Detailed theoretical study of the electron spectrum of the nano-structures under strong magnetic fields is therefore of primary importance for the future progress in this field . Initially the solutions for an electron in confined plane geometries, like a disc, ring, cylinder and oval shape stadium [3, 4, 5] were proposed. As it was shown in [5] , these models are relevant to the notion of the chaos in the level statistics and related thermodynamics of such systems. Among already studied three dimensional systems are electrons on simple surfaces as nanotubes [5, 6, 7]. A challenging problem is an adequate quantum mechanical description of noninteracting electrons on a nanoparticle of an arbitrary shape.
Here we consider a single electron confined to the surface of revolution placed in an axial uniform magnetic field . Our goal is to treat the general case of the arbitrary shaped surface of revolution 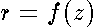( 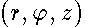are cylindrical coordinates) and to investigate influence of its geometrical characteristics upon quantum- mechanical spectrum. Further we suppose the surface to be smooth , closed and crossing 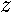-axes only in two points. The uniform magnetic field 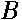is defined to point in the 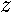-direction .
The problem is described by the Hamiltonian

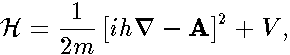(1)

where , for simplicity ,we ignore spin dependent terms . is the symmetric gauge , 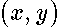are Cartesian coordinates. This is leading to the Schrodinger equation on the surface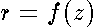

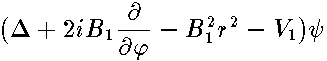
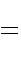
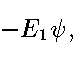
(2)

where: , .
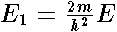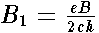
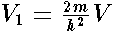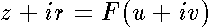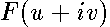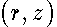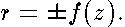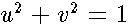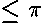
We introduce new orthogonal coordinates by , where the function maps conformally the domain of the -plane containing the unit circle onto the domain of the -plane containing the closed curve This curve is the image of the circle with the arc 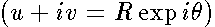corresponding to 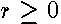. Since conformal mapping conserves a normal to the surface, it enables us to write the Eq. 2 on the surface 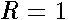neglecting derivatives in 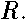Thus , the three dimensional Schrodinger operator has been reduced to a two-dimensional operator in 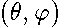-variables .
Due to conservation of the 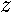-component of the angular momentum, the cyclic coordinate 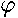can be separated in the Fourier series development

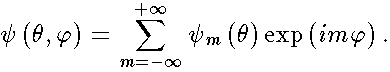(3)

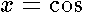
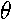Further simplification results in the ordinary differential equation of the second order

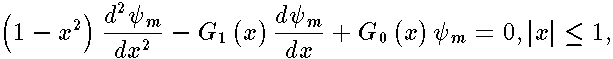(4)

Here : , ,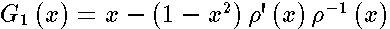

, , , .
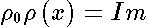
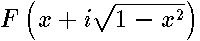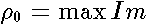
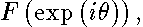
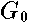
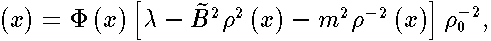
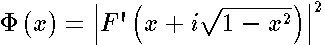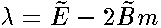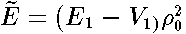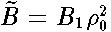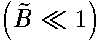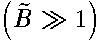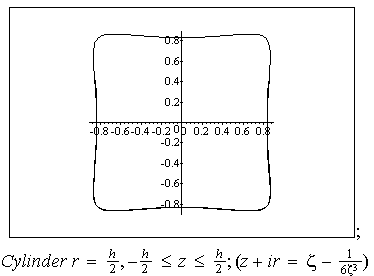
A low field asymptotics of the spectrum and eigenfunctions may be found in the traditional way by the pertubation method . It is much more difficult to suggest some general approach to indicate a high field asymptotics. This is governed by coefficients of the Eq. 4 or , in other words , by the surface shape. Some possible shapes and corresponding conformal mappings 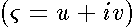are shown on Fig 1-10.,where conformal mappings are pointed out in the brackets.

.
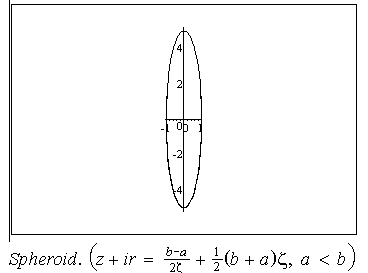
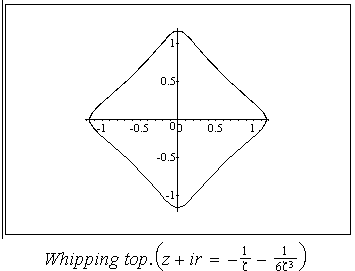
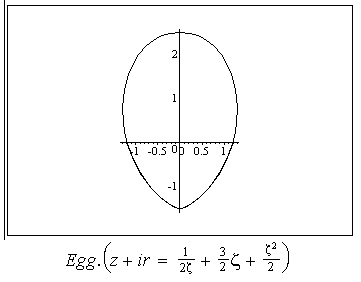
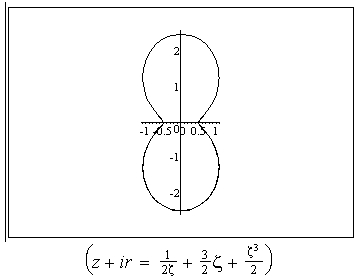
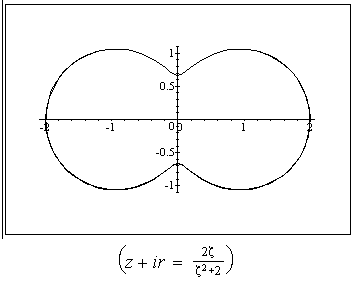
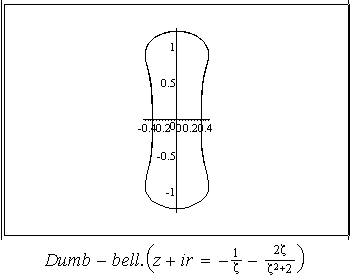
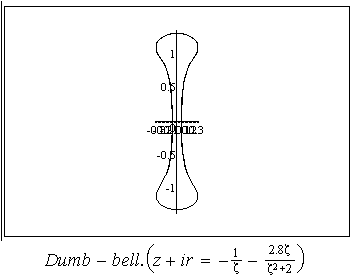
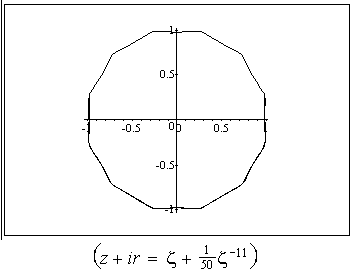
Below we consider closely a spheroidal surface whose equation is

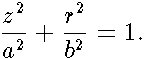(5)

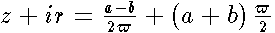
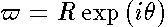
Conformal mapping: is an one-to-one mapping of the unit circle 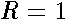onto this ellipse of the 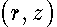-plane .
The Eq. 4 can be written in the form

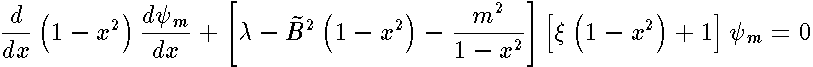(6)

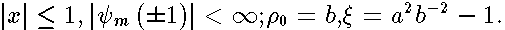
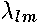This problem has an infinite discrete spectrum . Its eigenfunctions 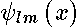have 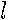zeroes in the interval 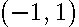. One can see, that if 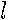is even (odd) integer, then these functions are even (odd) .
It can be shown that all eigenvalues 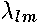are positive . They are large as one of the conditions : 1) 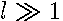, 2) , 3) , is fulfilled . Below we are pointing out leading terms of the corresponding asymptotics .
As 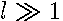, the spectrum can be obtained with the method of the paper [ 8 ]. Particularly , the leading term is given by

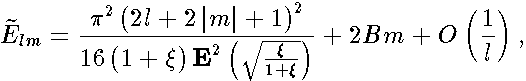(7)

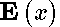where is a complete elliptic integral of the second kind .
As , the asymptotic expansion may be found with a stretched variable 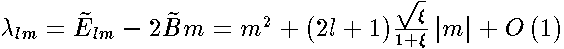.Eigenfunctions are expressed by Hermite polynomials ,
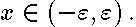
In the high field limit ( ) the spectrum is given by an asymptotic formula:

(8) The corresponding asymptotic expansion of the eigenfunctions is expressed by Laguere polynomials

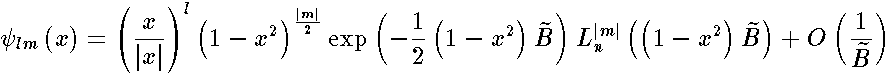
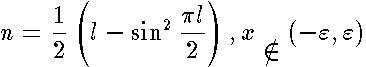
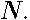Hence it appears that bunches of the energy levels resembling the Landau levels are formed in the high field limit. Every bunch consists of the parallel equidistant levels with the same number Their leading term is irrespective of a spheroidal geometry and coincide with the spectrum for the plane. The energy level corresponds to two quasi-degenerated bound states labele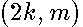d and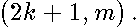
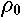A disk of the radius is a limiting case of a strongly flattened spheroidal shell (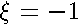). In this limit , the values of the eigenfunctions on both sides of the disk 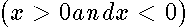are added and according to the above formula the antisymmetric eigenfunctions are cancelled out . Since 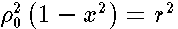, we obtain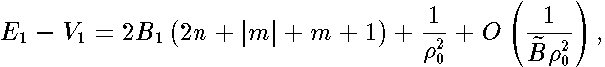

(9)

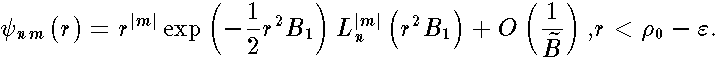
These relationships turns into the well known Landau solution as . In the high magnetic field the disc (circle billiard) spectrum coalesces into the straight lines nearly the same that in the classical Landau problem . This confirms results of the numerical calculations by K.Nakamura and H.Thomas [ 5 ].
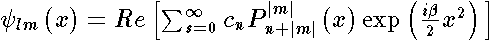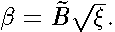In order to calculate the spectrum we represent by the expression , Here indices 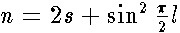are either even or odd integers corresponding to the to symmetric and antisymmetric solutions , respectively.
Substituting this expansion into the Eq. 6 yields two recurrence formulas (separately for even and odd integers )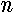

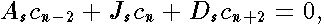(10)

where :

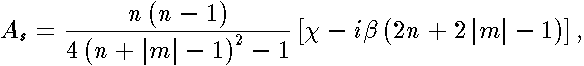
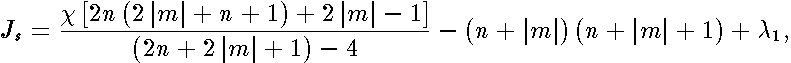
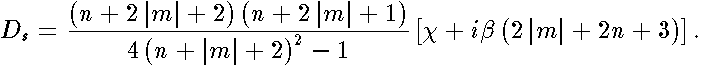
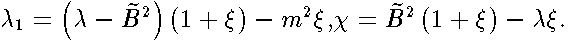
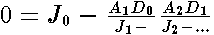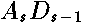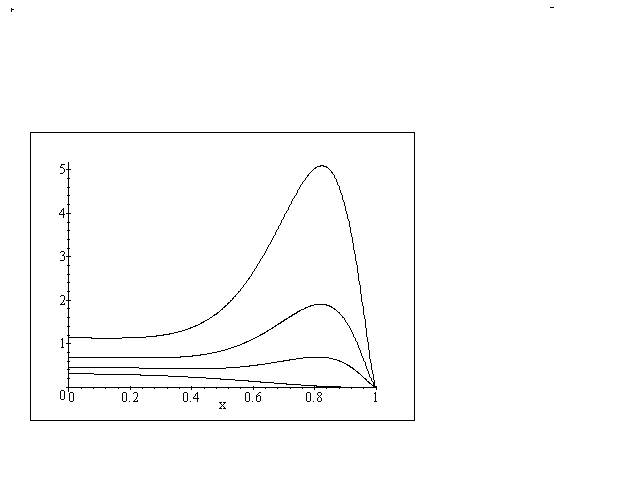
The spectrum is determined by equating the infinite determinants of these equations to zero and is given, therefore, by the roots of the following continued fractions . These continued fractions are real because are real values.
Results of the calculations are represented on the Fig 11-14.

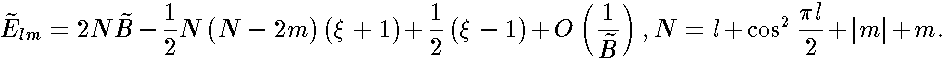
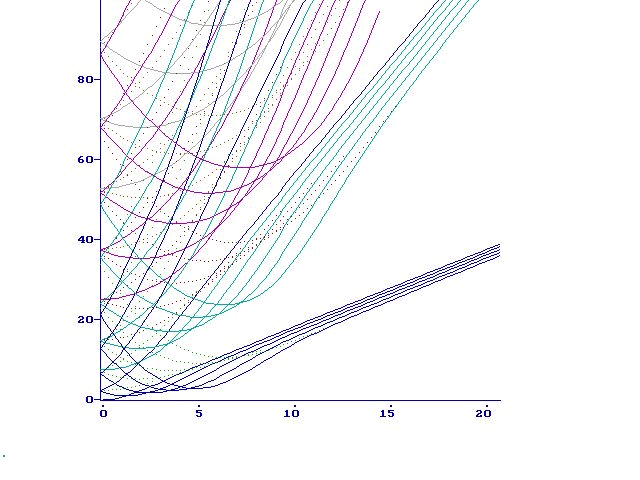
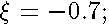
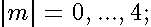
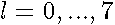
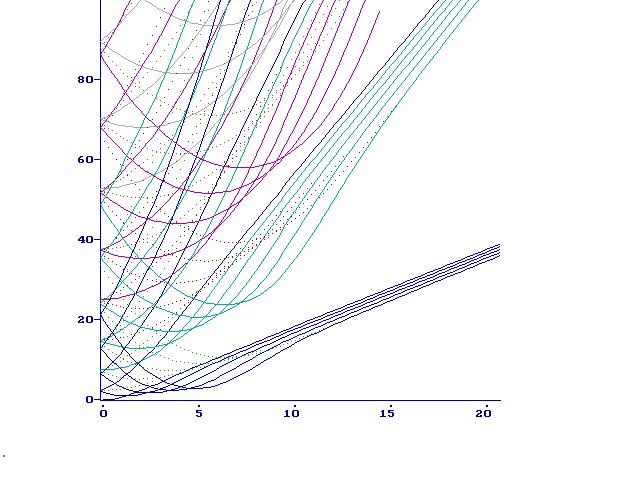
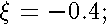
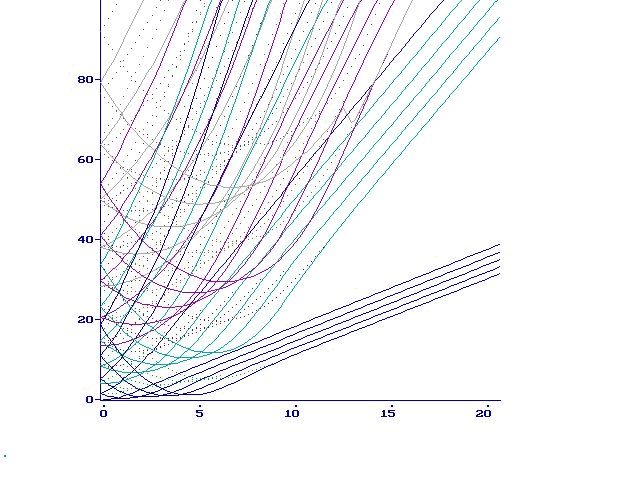
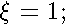
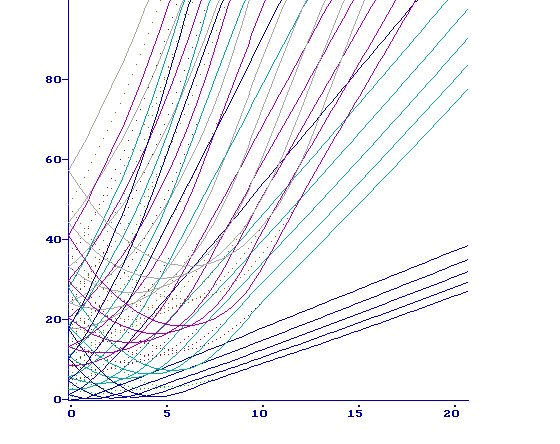
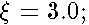
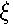We observe the behavior of the spectrum that was derived above analytically. As or increase, the distance between lines of the same bunch( the splitted Landau level) enlarges. Irregular crossings intensify as well. These crossings arise from dropping and intermingling lines of the different bunches.
Examples of the wave functions for the various parameters are shown on the Fig 15.

.

We may suggest that the electron motion on an arbitrary shaped convex surface has the spectrum behavior similar to the spectrum behavior of the electron on the spheroid. Especially, the chaotic location of the spectrum and numerous irregular crossings of the quantized energy levels is expected in a low magnetic field for the long enough surfaces. In the high field region the spectrum behavior is predetermined by the surface flatness in the vicinity of the poles (where the electron is trapped), and energy levels constitute bunches of the straight lines that coalesces into the Landau levels as the surface is strongly flat.

Bibliography

1. J.A.A.J. Perenboom, P. Wyder and F. Meier, Physics Reports, (1981)
   
2. J.M. van Ruitenbeck and D.A. van Leuwen, Phys. Rev. Lett., 67, 640 (1991).
   
3. M. Büttiker, Y. Imry and R. Landauer, Phys. Lett., 96A, 365 (1983).
   
4. D. Wohleben et al., Phys. Rev. Lett., 66, 3191 (1991).
   
5. K. Nakamura and H. Thomas, Phys. Rev. Lett. 61, 247 (1988).
   
6. Ju H. Kim, I.D. Vagner and B. Sundaram, Phys. Rev. B 46, 9501 (1992).
   
7. H.Aoki and H. Suezava, Phys. Rev. A46, R1163 (1992).
   
8. M.V.Fedorjuk, Diff.Equations, v.18, 2166-2173 (1982); v.19, 278-286 (1983).
   

---

WebMaster AK