 |
The Theory Group
Physics in High Magnetic Fields
I.D.Vagner Physics and Engineering Research Institute (P.E.R.I.)
|
| |
The Theory Group
Physics in High Magnetic Fields
I.D.Vagner Physics and Engineering Research Institute (P.E.R.I.)
|
,
with astonishing accuracy.
1.1 Lorentz invariance and finite frequency effects in the quantum Hall effect regime [7]
 | (1) |
is the current, 
is the electro- magnetic field strength tensor and 
are some coefficients. The relativistic invariance is preserved if the coefficients form a constant tensor. In D+1 space-time dimensions the only constant tensors are the metric tensor 
and the totally antisymmetric D+1 component tensor 
. In 3+1 dimensions it is impossible to construct a constant three component tenser, out of and _
, therefore the 3D macroscopic electrodynamics is not Lorentz invariant. In 2+1 dimensions, however, such a tensor may exist: 
. It is easy to see, that a physical system, discribed by Eq (2) is the QHE | (2) |
 | (3) |
 | (4) |
is the filling factor of the Landau levels and 
is the fine structure constant. Eqs.(2)-(4) could be cast, therefore, in a 2+1 dimensional vector equation:  | (5) |
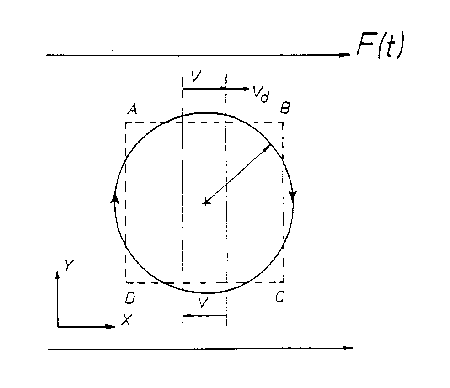
1.2 Time-dependent fields
.
, vanishing in the
plateau region, the imagionary part of the diagonal conductivity remains finite, due to
the polarization currents, and is linearly dependent on frequency:
.
The origin of the polarization currents, contributing to
is visualized in the figure. An electron
experiences
time dependent acceleration on the arcs (approximated by straight lines) AB and CD
and acquires a drift velocity along the electric field and a corresponding current.
1.3 Helicon Resonance in Doubly-Periodic-Multi-Quantum-Wells [2]
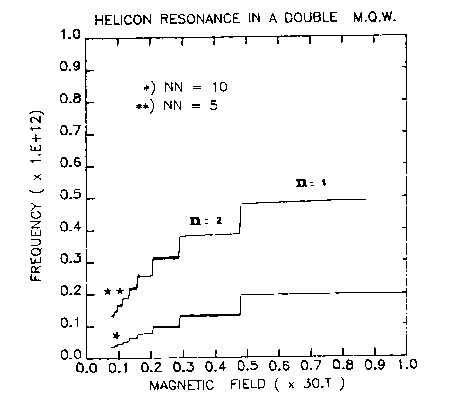Figure 1.
1.4 Interplateau region [3]
2.1 Spin excitons in periodic potentials
[9]3.1 Skyrmions in a 2D electron gas
at zero temperature 2DES under
strong magnetic field is equivalent to an isotropic 2D ferromagnet, which
can be described by a three component order parameter in a 2D coordinate
space, i.e. by a model known as the non-linear 
model .The
symmetry is known to be associated with some nontrivial topological
invariants , which can lead to spontaneous creation of unusual topological
point defects. At filling factor 
, for example, they have been shown
to be skyrmions . It has been shown by Sondhi et al. that the energy gap for
creation of a widely separated skyrmion-antiskyrmion pair, in this limit, is
the half of that needed to create a large spin exciton. Recent nuclear
magnetic resonance experiment , in which the local spin polarization of a 2D
electron system was directly measured, indicates the existence of such
states.
which is proportional to
the mean (macroscopic) value of the spin density operator was derived in the
limit when the spatial dependence of the corresponding rotation angles is
very smooth, on the magnetic length scale. This variational form is valid up
to second order in the characteristic wavenumber of the nonuniform rotation.
4.1 Finite size effects in FQHE
Two-dimensional electron gas (2DEC) under strong magnetic field have offered several unexpected experimental discoveries. Most notable are integer and fractional quantum Hall effects (QHE): precise quantization of the Hall resistance and zero diagonal resistivity at integer and fractional filling factors.
In the paper [1] the authors looked upon the known properties of 2DEG under strong magnetic fields from a novel point of view: the underlying symmetries of the macroscopic Maxwell equations. They found that in the plateau regions this system exhibits Lorentz and scaling symmetries, and estimated their exactness. They identified a possible symmetry breaking mechanism-polarization currents in ac QHE - and outlined how they can be measured in the helicon resonance in a superlattice with 2DEG. In the next paper [2] the wave propagation in a model superlattice with QHE conditions in the 2DEG layers separated by dielectric layers was considered. The standard method was used to reduce the Maxwell equations in a layered conductor with a perpendicular magnetic field to the Kronig-Penny like problem. It was found that at sufficiently low frequencies the helicon resonance exhibits flat plateaus simultaneously with sxy plateaus of the QHE. As the resonance frequency grows, the plateaus acquire a finite slope which increases with frequency and are eventually destroyed by the in-plane polarization currents.
Most of the published experimental data display the fractional QHE at odd-denominator filling factors. This is usually attributed to the formation of a homogeneous incompressible quantum liquid (the Laughlin state), which is not operative at filling factors with even denominators. When the fractional QHE at even-denominator filling factor was o@rved, a generalization of the Laughlin trial wave function which accounts for a spin mixing of higher Landai-i levels was made in order to explain these observations. Spontaneous breaking of the translational symmetry of 2DEG in strong magnetic fields may result, under certain conditions, in the lowering of its free energy.
The papers [3], [4] are devoted to the problem of stability of the homogeneous 2DEG in strong magnetic fields at even-denominator fractional occupations. An analytical method for calculations of energy gaps in clusters with arbitrary number of particles was developed, and is ,vas shown that small clusters (quantum lakes) have size-dependent energy gaps at any simple fractional filling factors.
The last papers of this part are devoted to the very important problem of the influence of scattering by impurities on the QHE plateaus. In the paper [5] the authors presented a simple scaling model of the magnetic field dependence of the transport coefficients in the interplateau regions, and demonstrated how the similarity between the transport coefficients may shed some light on the electron scattering mechanisms. Staxting with an assumption of a power-law dependence of the relaxation time and electron concentration in the interplateau region on the magnetic field a relationship between the relative indices was derived.
The calculation of the density of electronic states is of a primary importance for a proper understanding of the magnetotransport in 2DEG. Activity in the field of the magnetotransport properties of quasi-two-dimensional systems has introduced a new dimension into this problem. In these systems the motion of electrons along the direction perpendicular to the two-dimensional layers cannot be neglected and may play a significant role in the electron dynamics under the influence of a magnetic field. Accordingly, in the paper [6] the effect of non-magnetic impurity scattering on the Landau level width in a quasi-two-dimensional conductor was studied. It was shown that the square-root dependence of the Landau level width on a magnetic field obtained in the well known model of Ando and Vemura in 2DEG crosses over to a 2/3 power law in the case of a quasi-two-dimensional electron gas.
Bibliography
[1] B. Rosenstein and I.D. Vagner. J. Phys.: Condens. Matter, 2, 497 (1990).
[2] I.D. Vagner and D.J. Bergman. "RF Quantum Hall Effect in a Superlattice". Phys. Rev. B35, 9856 (1987).
[3] B. Rosenstein and I.D. Vagner "Clusters in 2D-Electron Gas at Even Denominator Filling Factors". Phys. Rev. B40 1973 (1989).
[4] I. D. Vagner, B. Rosenstein Quantum lakes at Half-Filling of the Ground Landau Level. 20th International Conference on the Physics of Semiconductors, v.2. Thessaloniki, Greece, August 6 - 10, 1990. Ed. E.M. Anastassakis, J.D. Joannopoulos. World Scientific. Singapore.
[5] I. D. Vagner and M. Pepper "Similarity Between Quantum Hall Transport Coefficients". Phys. Rev. B.37 , 7147 (1988).
[6] T. Maniv and I.D. Vagner "Broadening of the Landau Levels in Q2D Conductors due to Impurity Scatt". Phys. Rev. B38 6301 (1988).
6. 2DEG under strong magnetic fields
2DEG under strong magnetic fields exhibits at odd integer filling factors a strong electron spin polarization. It is thus a unique system for investigating of the interplay between the spin and orbital degrees of freedom in 2DEG under the conditions of QHE. In the single-electron approximation, the spin up and spin down electrons are separated by an energy gap equal to the "bare" Zeeman spin splitting energy |g| mBBwhere g is the "bare" g-factor, which is different from the free electron g-factor g0 due to the crystal fields. The electron-electron interaction changes this simple picture drastically. Due to the Coulomb interaction, the low lying excitations are electron - hole pairs of opposite spins (spin excitons) which, unlike the individual electrons or holes, have a nonzero kinetic energy and strong dispersion in the wave vector k. These elementary excitations are therefore chargeless particles with neaxly parabolic dispersion in the low k limit. At k = 0 there exists a gap equal to the bare Zeeman splitting. The invariance of the energy gap with respect to the electron - electron interaction is associated with the fact in creating a quasi-electron - quasi-hole pair excitation at the same point in space (i.e., with the exciton momentum k = 0 ) the energy decrease due to the Coulomb attraction is exactly canceled by the deficite in the exchange energy connected with the creation of holes on the fully filled Landau sublevel.
An interesting possibility may arise, if one uses a novel technique in which 2DEG is exposed to an artificially generated periodic potential with periods in submicron range. In the papers [1], [2] it was shown that the spin-exciton band structure in a periodically modulated 2DEG under strong magnetic fields is unusually rich due to the peculiar nature of the free exciton dispersion law. It was found that the periodic modulation potential can distort the single spin-excitonic state so strongly that the energy gap in the spectrum can disappear. The system exhibits a peculiar discrete spectrum near the bottom of the spin-exciton band. The combined effect of the electrostatic modulation potential and the electron - hole Coulomb attraction under the magnetic field leads to nearl bound relative electron - hole oscillations perpendicular to the modulation axis which have a characteristic Rydberg-like spectrum near the edge of the spin-exciton band. The energy gap for creating of a widely separated quasielectron - quasihole pair, or a large spin-exciton (i.e., the one with k -> oo), is apart from the Zeeman splitting governed by the energy exchange associated with a hole, results in a strong enhancement of the effective g-factor. Recent theoretical investigations, however, revealed that the interplay between Zeeman and Coulomb interaction results in a more complicated type of excitations with unusual spin order which can be described as Skyrmions.
In the paper [3] the Hartree - Fock (HF) approach was presented which can treat all types of spin excitations within the same framework and thus clearly shows the connection between Skyrmionic excitations and the more common spin excitations, i.e., spin excitons. Using the linear momentum representation a canonical u-v transformation was constructed from the fully polarized ground state to a state consisting of a macroscopic number of differently oriented spins each of which is slightly rotated with respect to its nearest neighbors in space. In the limit when the spatial dependence of the corresponding rotation angles is very smooth on the magnetic length scale, a variational form for the Hamiltonian part of the HF energy of the system expressed in terms of a unit vector field which is proportional to the mean value of the spin-density operator was derived. In the paper [4] the effective Lagrangian was derived. Microscopic deviation of the kinetic part reveals a nonzero Hopf term, the prefactor of which shows that the Skyrmion caxries a spin 1/2. In the next paper [5] the effect of a weak Zeeman splitting on the spatial distribution and the energy of an isolated Skyrmion was studied. Finite Zeeman splitting introduces two different characteristic lengths into the problem corresponding to the tail and the core of the spin distribution. In the limit of a very small g-factor the tail of the Skyrmion is much longer than its core radius.
In the paper [6] another approach to the problem of Skyrmions is offered by using transformation induced by application of a non-reduced to the same Landau level states rotation matrix and considering the full Schrodinger equation obtained by means of ordinary perturbation theory applied to the gradients of this matrix. The propagation of spin waves in the presence of a single Skyrmion in the framework of the proposed approach was considered. A spatial branch of collective excitations was found corresponding to oscillations of the Skyrmion core size.
Bibliography
[1] Yu. A. Bychkov, T. Maniv, I.D. Vagner and P. Wyder "Gapless Spin-Excitons in Periodically Modulated Two-dimensional Electron Gas. " Phys. Rev. Lett. 73, 2911 (1994).
[2] Yu. A. Bychkov, T. Maniv, I.D. Vagner and P. Wyder "Narrow resonance states of 2D magnetic spin-exciton in periodically modulated fields. " Europhys. Lett., 40, 557 (1997).
[3] Yu. A. Bychkov, T. Maniv and I.D. Vagner "Charged skyrmions: A condensate of spin excitons in a two-dimensional electron gas. " Phys. Rev. B 53 , 10148 (1996).
[4] W. Apel and Yu.A. Bychkov "Hopf Term and the Effective Lagrangian for the Skyrmions in a Two-Dimensional Electron Gas at Small g Factor. " Phys. Rev. Lett. 78, 2188, 1997.
[5] Yu. A. Bychkov, A.V. Kolesnikov, T. Maniv and I.D. Vagner "Spatial Spin Distribution of a Skyrmion in 2D Electron Gas at a Small g-factors. " J. Phys. Condensed Matter, 10, 2029 (1998).
[6] S.V. Iordanski "Collective excitations of a single skyrmion in two dimensions at high magnetic field. " J. Phys.: Condens. Matter, 10, 247 (1998).
| Main Page | Visitors | Projects | Links |
