The Theory Group

Physics in High Magnetic Fields

I.D.Vagner

Grenoble High Magnetic Field Laboratory (CNRS-MPI)
166X, F-48042, Grenoble, Cedex 9, France.
Tel: +33-4-76-88-11-27; Fax: +33-4-76-85-56-10.
E-Mail: vagner@labs.polycnrs-gre.fr

Physics and Engineering Research Institute (P.E.R.I.)
Ruppin Instutute for Higher Education
Emek Hefer 40250, Israel.
Tel: (+972)-9898-1340, (+972)-9898-3042;
Fax: (+972)-9898-6848
E-mail: perinst@netvision.net.il


Hyperfine interaction

  1. Quantised Nuclear Spin Relaxation Effect
  2. The Hyperfine Interaction Driven Anomalous Hall Effect
  3. Hyperfine Interaction and Residual Resistivity in Normal and Ferromagnetic Metals

1. Quantised Nuclear Spin Relaxation Effect

It was outlined in [1] that in two-dimensional electron systems under strong magnetic fields the contact hyperfine interaction, resulting in the simultaneous spin flip of the nuclear and the electron spins (flip-flop) (Fig.1) is severely restricted by energy conservation, since the electron spin splitting is orders of magnitudes larger than the nuclear one.

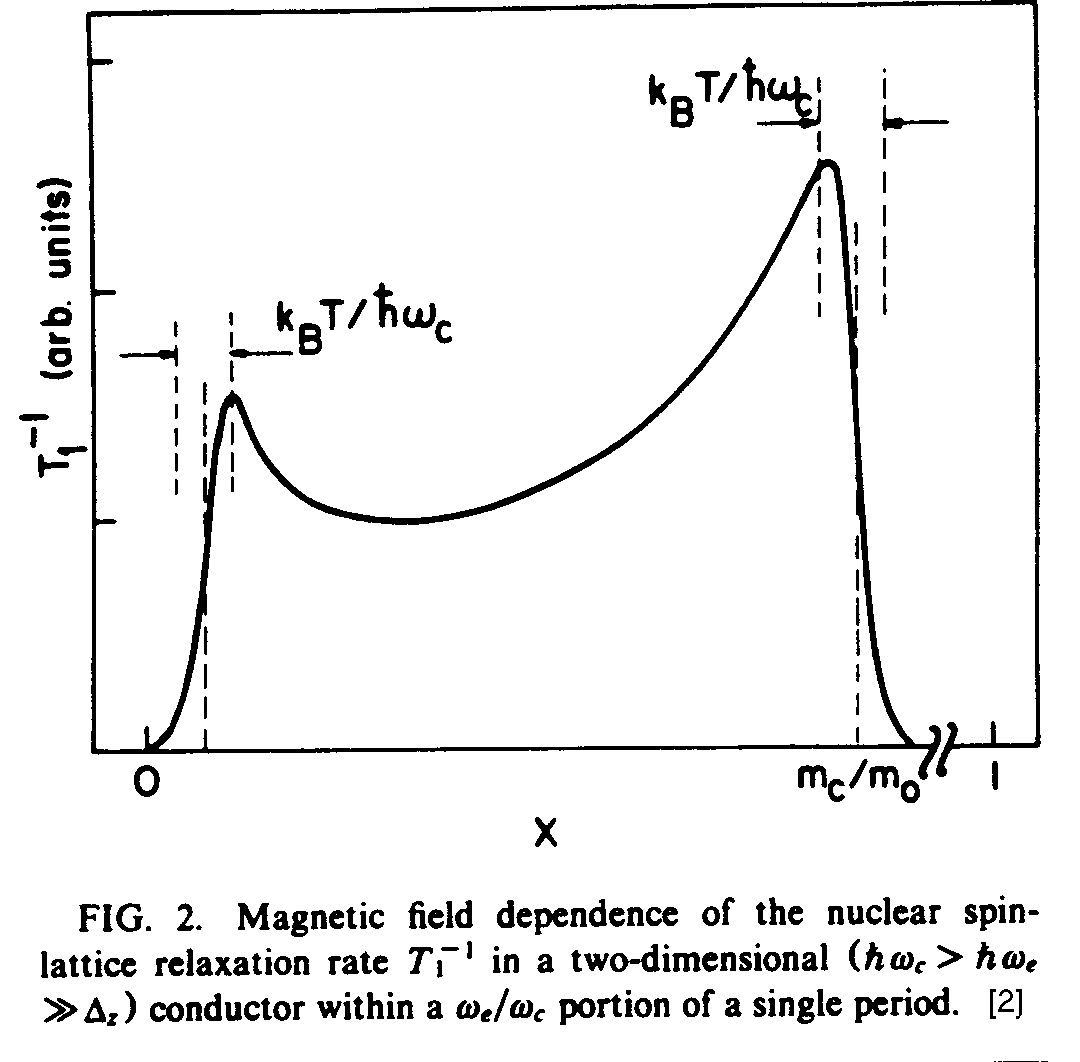
It was shown in [2] that the discreteness of the electron spectrum will manifest, therefore, in an activation type of the magnetic field dependence of the nuclear spin relaxation rate, (Fig.2) , similar to that of the magnetoresistance in QHE (QNSRE - quantised nuclear spin relaxation effect).

[From: A.Berg,M.Dobers,R.R.Gerhardts and K.v.Klitzing,
Phys.Rev.Lett. 64, 2563 (1990)]

The measurement of the nuclear spin-relaxation in heterojunctions is a challenging experimental problem, since the number of nuclear spins interacting with the two-dimensional electrons is negligibly small compared to their total number in a sample. Nevertheless, the magnetic field dependence of under QHE conditions was measured, using the Overhauser effect, in a series of elegant experiments by the K. von Klitzing group, (Fig.3). These measurements shows close similarity between the magnetic field dependence of the nuclear spin-relaxation rate and the magnetoresistance in quantum Hall effect, as it was predicted in [2] thus demonstrating clearly the importance of the coupling of nuclear spin to the conduction electron spins in the nuclear relaxation in these systems.

Because of existence of the energy gap in the electron spectrum, finite nuclear relaxation times could be expected only if 2DES is subjected to different kinds of external potentials, as the short range impurities [3], long range potential fluctuations in a heterojunction[5,7], and edge states [8]. At relatively high temperatures a phonon assisted mechanism for relaxing the polarized nuclear spins can be operative [12]. In very clean limit the alternative relaxation channels, like the magnetic electron-nuclei interaction (dipolar), may start to be operative [10]. The dipole-dipole interaction does not conserve the total spin, and is not sensitive, therefore, to the existence of the Zeeman gap in the electron spectrum. In [14] a new mechanism for indirect nuclear spin transport via the exchange of virtual electron-hole pairs (spin excitons, ) is suggested.

Especial role of the edge states providing a homogeneous electronic spectrum for the nucllear spin relaxation (Fig.4) is studied in [8]. Ingenious transport measurements by McEuen group have demonstrated the possibility of studying the edge states by using the hyperfine interaction between the nuclear and electron spins.

Very recently combined optical and NMR technics were successfully applied to measure the nuclear spin relaxation in multi-quantum wells . In these measurements the low lying spin excitations near were identified as Skyrmions, topological point defects in the electron spin system which can be described by the nonlinear O(3) model.

2. The Hyperfine Interaction Driven Anomalious Hall Effect

While the hyperfine field of polarised nuclei acts, via the contact hyperfine interaction, on the conduction electron spins only, the inclusion of the spin-orbit coupling results in a modification of the electron kinetic momentum. It was shown [18], that the interplay of the nuclear polarisation and spin-orbit coupling leads to oscillatory effects similar to the Aharonov-Bohm effect in mesoscopic systems. A very important question is whether, in systems with strong spin-orbit coupling, like the GaAs/AlGaAs heterojunctions, the nuclear spin polarisation may introduce corrections to the conductivity tensor, and/or influence the quantum Hall effect.

Anomalies of the Hall effect were observed long ago in ferromagnetic metals as well as antiferromagnetic metals and semiconductors. It has been generally recognised that the spin-orbit interaction is responsible for this effect. Due to this interaction, electrons with their spin polarisation parallel to the magnetisation axis will be deflected at right angles to the directions of the electric current and of the magnetisation while electrons with antiparallel spin polarisation will be deflected in the opposite direction. Thus, if the two spin populations are unequal, a net current appears in the transverse direction which, in the Hall geometry, has to be cancelled out by the Hall voltage. Our hypothesis that the AHE can also exist in two dimensional system is simply based on the fact, that the 2DEG is affected by the spin-orbit coupling due to the electric field at the heterojunction interface and/or due to the lack of inversion symmetry in the unit cell of the bulk material. This spin-orbit interaction gives rise to a splitting of the conduction subbands even in zero magnetic field and has been studied experimentally and theoretically.

The work performed is focused on the exploration of a simple idea, which has not been considered up to now. This is to look for the anomalous Hall effect (AHE) in the presence of polarised nuclei and without an external magnetic field. The role of the contact hyperfine interaction is to replace the external magnetic field which splits the conduction band and creates the magnetisation of the carriers. This gives the possibility to observe the genuine spin dependent anomalous Hall effect not hidden by the much larger ordinary Hall effect. By polarising the nuclei in the sample before the measurement, an effective hyperfine field of the order of 1T can be created, which slowly decays with time as the nuclei relax. In semiconductors at sufficiently low temperature the nuclear spin relaxation time can be of the order of an hour. Taking advantage of the fact that the nuclear spin polarisation naturally relaxes one can observe the time evolution of the AHE and separate it from the time independent ordinary Hall effect which is considerably weaker.

3. Hyperfine Interaction and Residual Resistivity in Normal and Ferromagnetic Metals

URR: Universal Residual Resistivity due to Hyperfine Interaction in Metals

One of the most fundamental questions in the electronic transport in solids is to which extend the purity of the sample defines the electron mean free path. At low temperatures, when the phonon scattering is eliminated, the main contributions to resistivity are impurities and electron interactions. It is believed that when the impurity concentration is sufficiently low, the resistivity should have a temperature dependence . Scattering by magnetic impurities results in widely studied Kondo effect, which yields a nonanalytic in contribution to resistivity. Much less attention attracts the magnetic scattering of conduction electrons by nuclear spins. It was observed experimentally in strongly doped semiconductors, and is usually neglected in metals. There is however strong evidence that conventional scattering can not explain anomalies in residual resistivity at low temperature.

We have suggested [17], that the hyperfine interaction between the conduction electron spins and nuclear spins may result in universal residual resistivity in clean metals at low temperatures. Apart of the fundamental nature of this problem, the natural limitations on the mean free path are decisive in the semiconductor based high speed electronic devices, like heterojunctions and quantum wells.

We have performed a theoretical study of the contribution of the hyperfine contact (Fermi) interaction between the conduction electrons and nuclear spins to the temperature and magnetic field dependence of resistivity . It follows that as a result of electron-nuclear interaction the residual resistivity in isotopically clean metals is not vanishing even when the impurity concentration (the universal residual resistivity, URR), as long as the nuclear spins are disordered. In this temperature interval URR reflects the existence of an upper limit for the mean free path of conduction electrons. This scattering is not operative at extremely low temperatures in Cu, for example) when the nuclear spins are ordered.


  1. I.D. Vagner, T. Maniv and E. Ehrenfreund ''Prediction of Strong Magnetic Quantum Oscillations of the Nuclear Spin Relaxation In a Quasi-Two-Dimensional Metal.'' Solid State Commun. 44, 635 (1982).
  2. I.D. Vagner and T. Maniv ''Nuclear Spin Lattice Relaxation: A Microscopic Probe for Systems Exhibiting the Quantum Hall Effect''. Phys. Rev. Lett. 61,1400 (1988).
  3. T. Maniv and I.D. Vagner ''Nuclear Spin-Lattice Relaxation in Quasi - 2d Systems: The Role of Impurity Scattering''. Surf. Sci. 229,134 (1990).
  4. R. Wessel and I.D. Vagner ''Spin-flip Assisted Resonant Tunneling''. Superlattices and Microstructures, 8,443 (1990).
  5. S.V. Iordanskii, S.V. Meshkov and I.D. Vagner ''Relaxation of nuclear spin in a 2D electron gas''. Sov. Phys. - JETP. Lett. 53,381 (1991).
  6. V.I. Fal'ko, S.V. Meshkov and I.D. Vagner ''On the Relaxation of Nuclear Polarisation Near 2D Electron Gas''. J. Phys.: Condens. Matter 3,5079 (1991).
  7. S.V. Iordanskii, S.V. Meshkov and I.D. Vagner ''Nuclear Spin Relaxation and Magnetoexcitons in a 2D Electron Gas''. Phys. Rev. B44,6554 (1991).
  8. I.D. Vagner, T. Maniv et T. Salditt ''Nuclear Spin-Lattice Relaxation Under the QHE Conditions in the Edge States'' (in: High Magnetic Fields in Semiconductor Physics III, 101, 131 (1992); Ed. G. Landwehr, Springer-Verlag Berlin Heidelberg.)
  9. Yu. A. Bychkov, T. Maniv, I.D. Vagner and P.Wyder, ''A New Mechanism for the Nuclear Spin Depolarization in a Spin Diode'' JETP Lett. 58, 788 (1993).
  10. Yu. N. Ovchinnikov, I.D. Vagner and A. M. Dyugaev, ''Nuclear Spin Relaxation via Dipolar Interaction in a Two-dimensional Electron Gas'' JETP Lett., 59, 569 (1994).
  11. A. M. Dyugaev, I.D. Vagner and Yu. Ovchinnikov, ''Dynamic Polarization of Liquid 3He at High Temperature'' JETP Lett., 59, 640 (1994).
  12. Ju H. Kim, I.D. Vagner and L. Xing ''Phonon Assisted Mechanism for Quantum Nuclear Spin Relaxation'' Phys. Rev. B49,16777 (1994).
  13. I.D. Vagner and T. Maniv, ''Hyperfine Interaction in Quantum Hall Effect Systems (Review)'' Physica B204, 141 (1995).
  14. Yu. A. Bychkov, T. Maniv and I.D. Vagner ''Nuclear Spin Diffusion via Spin-Excitons in the Quantum Hall Effect Regime'' Solid State Commun.94, 61 (1995).
  15. I.D. Vagner, Yu. A. Bychkov, A.M. Dyugaev and T. Maniv ''Hyperfine interactions and spin textures in quantum Hall systems'' Physica Scripta, T66, 158 (1996). (Invited talk at EPS 15-th General Conference of the CMD).
  16. A.M. Dyugaev, I.D. Vagner and P. Wyder ''Contribution of the electron-nuclear interaction to the residual resistivity.'' JETP Lett. 64, 207 (1996)
  17. A.M. Dyugaev, I.D. Vagner and P. Wyder ''Concurence between the nuclear magnetism and superconductivity.'' JETP Lett. 65, 811 (1997).
  18. I.D. Vagner, A.S. Rozhavsky, P. Wyder and A.Yu. Zyuzin ''Is the magnetic field necessary for the Aharonov-Bohm effect in mesoscopics?'' Phys. Rev. Lett. 80, 2417 (1998)



Main Page Visitors Projects Links




Last updated 19-Jan-01.
WebMaster AK