 |
The Theory Group
Physics in High Magnetic Fields
I.D.Vagner Physics and Engineering Research Institute (P.E.R.I.)
|
 |
The Theory Group
Physics in High Magnetic Fields
I.D.Vagner Physics and Engineering Research Institute (P.E.R.I.)
|
1.1 Magnetization oscillation envelope
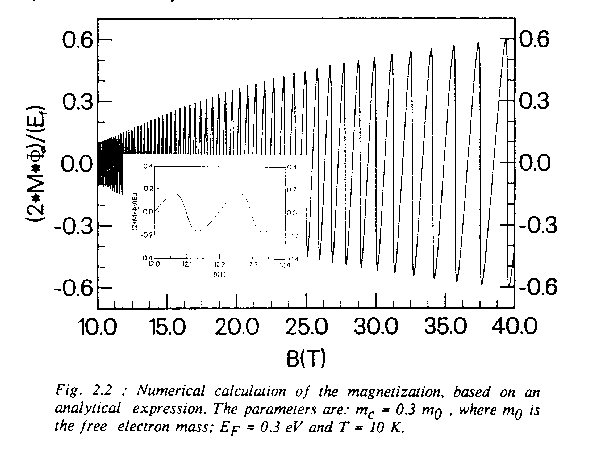
1.2 The reservoir model
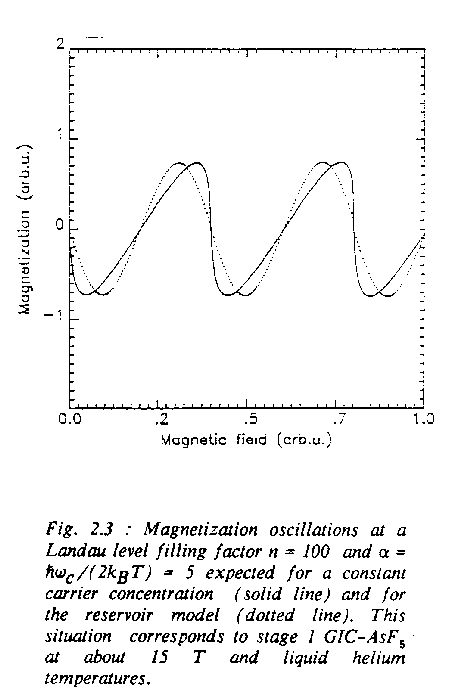
2. Strong Coulomb Correlations and Lattice Effect on dHvA Oscillations
|
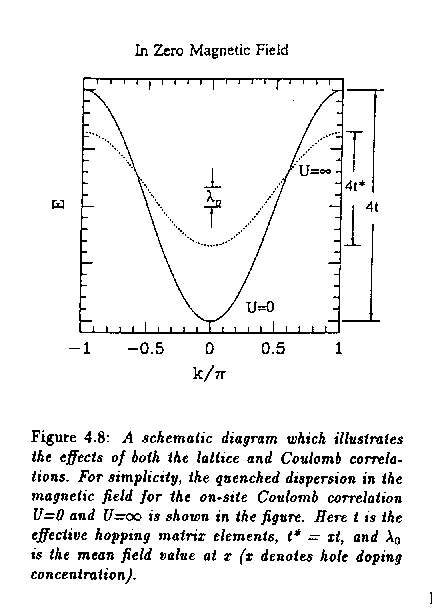
Lattice effects Coulomb interactions
|
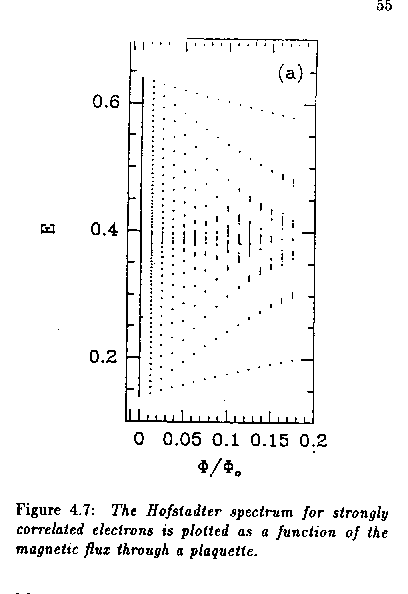
|
Magnetization oscillations
 |
 |
Electron- phonon intractions
| Main Page | Visitors | Projects | Links |